10진법 수를 2진법, 8진법, 16진법으로 나타내는 방법과 n진법 수를 10진법 수로 바꾸는 방법을 정리해보려 한다.
먼저, 2진법, 8진법, 16진법에 대해 간단하게 살펴보면 다음과 같다.
2진법은 0과 1로만 수를 나타내는 방법이다. 2진법으로 나타낸 수에서 각 자리는 뒤에서부터 $2^0$, $2^1$, $2^2$, $2^3$... 의 개수로 생각하면 쉽게 이해할 수 있다.
- 0 = 0 = $(0 \times 2^0)$
- 1 = 1 = $(1 \times 2^0)$
- 2 = 10 = $(1 \times 2^1 + 0 \times 2^0)$
- 3 = 11 = $(1 \times 2^1 + 1 \times 2^0)$
- 4 = 100 = $(1 \times 2^2 + 0 \times 2^1 + 0 \times 2^0)$
- 5 = 101 = $(1 \times 2^2 + 0 \times 2^1 + 1 \times 2^0)$
- 6 = 110 = $(1 \times 2^2 + 1 \times 2^1 + 0 \times 2^0)$
- 7 = 111 = $(1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0)$
- 8 = 1000 = $(1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0)$
8진법은 0부터 7까지의 수로 나타내는 방법이다.
- 8 = 10 = $(1 \times 8^1)$
- 9 = 11 = $(1 \times 8^1 + 1 \times 8^0)$
- 10 = 12 = $(1 \times 8^1 + 2 \times 8^0)$
- 11 = 13 = $(1 \times 8^1 + 3 \times 8^0)$
- 12 = 14 = $(1 \times 8^1 + 4 \times 8^0)$
- 13 = 15 = $(1 \times 8^1 + 5 \times 8^0)$
- 14 = 16 = $(1 \times 8^1 + 6 \times 8^0)$
- 15 = 17 = $(1 \times 8^1 + 7 \times 8^0)$
- 16 = 20 = $(2 \times 8^1 + 0 \times 8^0)$
16진법은 0~9까지는 숫자로, 10~15는 A~F로 표현하는 방법이다.
10에서 15를 그대로 숫자로 나타내면 16진법으로 나타낸 16이 10이기 때문에 헷갈릴 수 있어 알파벳으로 표현한다.
- 10 = A
- 11 = B
- 12 = C
- 13 = D
- 14 = E
- 15 = F
- 16 = 10 = $(1 \times 16^1 + 0 \times 16^0)$
- 17 = 11 = $(1 \times 16^1 + 1 \times 16^0)$
- 18 = 12 = $(1 \times 16^1 + 2 \times 16^0)$
- 19 = 13 = $(1 \times 16^1 + 3 \times 16^0)$
10진수 11을 2진법, 8진법, 16진법으로 나타내기 위해서는 각각 bin(), oct(), hex() 함수를 사용하면 된다.
함수의 이름은 영어 단어의 앞자리에서 가져온 것이다.
- 2진수 - binary
- 8진수 - octal
- 10진수 - decimal
- 16진수 - hexadecimal
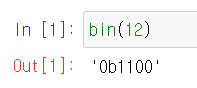
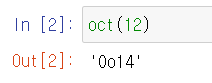

실행 결과, 리턴되는 값의 앞에 0b, 0o, 0x 가 붙어있는 것을 볼 수 있다.
이는 각각 2진수, 8진수, 16진수라는 것을 의미한다.
bin, oct, hex 함수의 결과는 문자열(str)로 리턴되기 때문에 단순히 값만 알고 싶다면 슬라이싱을 사용하여 값만 추출할 수 있다.
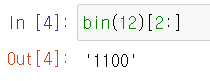

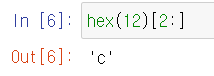
반대로, 2진법, 8진법, 16진법으로 나타낸 수를 10진수로 바꾸려면 어떻게 해야 할까
int() 함수를 사용하면 된다.
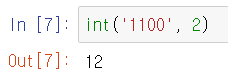

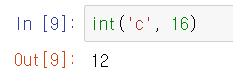
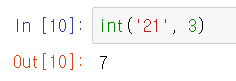
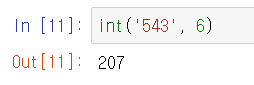
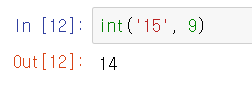
int(n진법 수, n) 형태로 작성해주면 10진수 결과가 출력된다. 이 결과는 당연히 정수값이다.
2진법, 8진법, 16진법이 아닌 수도 int 함수를 사용하면 10진수로 바꿀 수 있을까?
당연히 가능하다.