파이썬에서 순열과 조합을 사용할 수 있는 두 가지 방법을 정리해보려 한다.
먼저, 순열과 조합의 정의를 살펴보면 다음과 같다
- 순열(permutation): n개 중 r개를 선택하여 순서대로 정렬
- ex) 1, 2, 3에서 2개를 선택하여 순서대로 정렬 → (1, 2), (2, 3), (3, 1)
- (1, 2)와 (2, 1)을 같은 것으로 봄
- $_nP_r=\frac{(n-r)!}{n!}$
- 조합(combination): n개 중 r개를 선택 (순서 X)
- ex) 1, 2, 3 에서 2개를 선택 → (1, 2), (2, 1), (2, 3), (3, 2), (1, 3), (3, 1)
- (1, 2)와 (2, 1)을 다른 것으로 봄
- $_nC_r=\frac{(n!}{(n-r)! r!}$
1) math 라이브러리에 있는 perm, comb 메소드를 이용

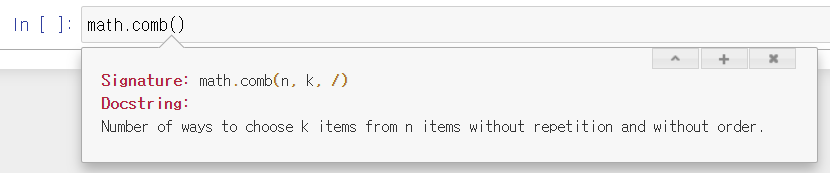
math.perm(): n개의 아이템에서 k개를 선택하는 방법(중복 X, 순서 O)
math.comb(): n개의 아이템에서 k개를 선택하는 방법(중복 X, 순서 X)
* 여기서 말하는 중복이란, n개의 주머니에서 k개를 뽑았을 때 다음번 뽑기에서 k개를 다시 넣고 뽑는 것을 말한다.
[1, 2, 3]이 있을 때 중복을 허용하여 2개를 뽑아 정렬하면(= 중복순열) (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)과 같은 결과가 나오게 된다.
중복을 허용했기 때문에 1을 뽑고 난 후 다시 1을 주머니에 넣어 1을 뽑을 수 있기 때문에 (1, 1)이라는 결과가 나올 수 있는 것이다.
여기서는 중복을 허용하지 않는 순열과 조합을 살펴본다.
직접 코드를 입력해 보면 다음과 같은 결과를 볼 수 있다.
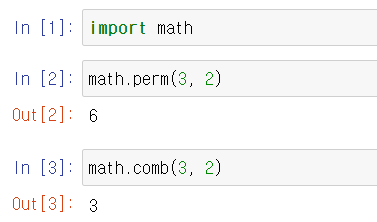
2) itertools 라이브러리에 있는 combinations, permutations 이용


여기서 iterable의 의미는 요소를 하나씩 차례로 반환 가능한 object를 말한다.
예시로 주어진 range(3)과 같이 0에서 2까지 순서대로 방문할 수 있는 매개변수가 combinations, permutations에 전달되어야 한다.
직접 코드를 입력해 보면 다음과 같다.


itertools의 permutations와 combinations는 math 라이브러리의 perm, comb와 다르게 itertools.permutations, itertools.combinations 객체를 반환하기 때문에 결과를 눈으로 보기 위해서는 list로 감싸주어야 한다.
오른쪽 코드처럼 리스트를 전달해 주면 리스트에서 r(= 2) 개를 선택하는 경우의 수를 모두 구할 수 있다.
정리
'3개의 구슬 중 2개를 선택하는 방법'과 같이 정확한 수가 주어진 경우라면 math.perm 또는 math.comb을 사용하는 것이 적합하고
'[1, 2, 3]에서 2개를 선택하는 방법'과 같이 리스트 또는 범위가 주어진 경우라면 itertools 라이브러리의 permutations 또는 combinations를 사용하는 것이 적합하다고 생각된다.