프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
처음 시도한 코드
import sys
sys.setrecursionlimit(10**6)
def fibo(x):
if x == 0:
return 0
elif x == 1:
return 1
else:
return fibo(x-1) + fibo(x-2)
def solution(n):
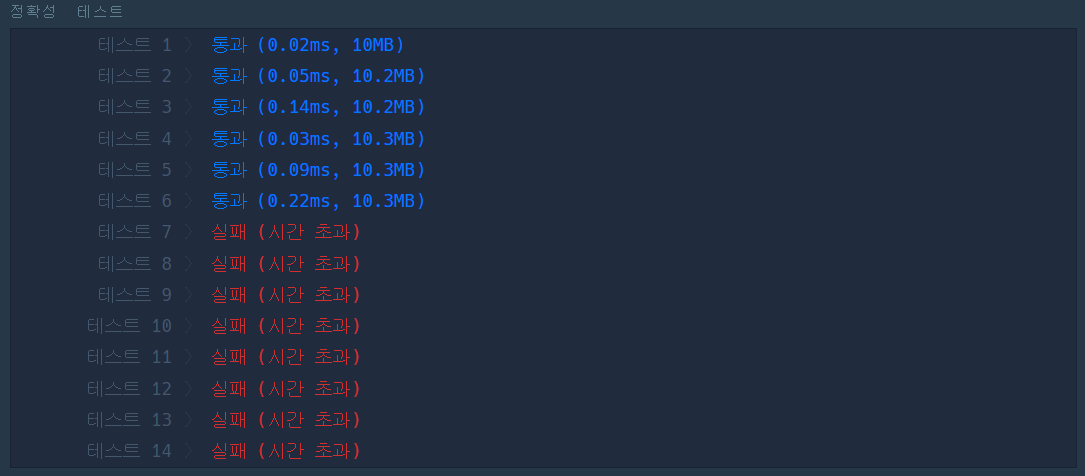
return fibo(n) % 1234567문제 이름을 보자마자 피보나치 함수 정도는 쉽게 구현할 수 있지!라고 생각했지만 결과는 처참했다.
런타임 에러도 아닌 시간초과를 맞닥뜨려 너무나 당황스러웠다. 어떻게 해결해야 할지 하나도 감이 잡히지 않았다..
힌트를 찾기 위해 여기저기 돌아다니다 재귀함수가 시간 초과의 원인이라는 것을 알게 되어 코드를 수정하게 되었다.
정답 코드 - 1) list 이용
def solution(n):
answer = [0, 1]
for i in range(2, n+1):
answer.append(answer[i-1]+answer[i-2])
return answer[-1] % 1234567재귀함수와 같은 역할을 하도록 배열을 사용해 n번째 피보나치 수를 구하기 위해 n-1번째, n-2번째 피보나치 수를 더해 배열에 추가하는 방법이다.
정답 코드 - 2) swap 이용
def solution(n):
a, b = 0, 1 # F(0), F(1)
for i in range(n):
a, b = b, a+b
return a % 1234567이 코드를 보고 이해하기까지 시간이 꽤 오래 걸렸다.
a, b를 0, 1로 초기화하는 것까지는 모두가 이해할 것이다. 하지만 왜 for문을 n번이나 반복하는지 이해하지 못했다.
그래서 또 직접 하나씩 경우를 세보았다.
- i=0, a=1, b=1 / F(3) = F(1) + F(2)
- i=1, a=1, b=2 / F(4) = F(2) + F(3)
- i=2, a=2, b=3 / F(5) = F(3) + F(4)
- ...
- i=n-1, F(n+2) = F(n) + F(n-1)
for문을 n번 반복하면 최종적으로는 F(n+2)를 구하는 것과 같아진다.
각 회차에 a와 b는 F(n), F(n-1)을 나타내기 때문에 n-1번째 즉, F(n+2) 일 때 a값이 F(n)이 된다.
따라서 구하고자 하는 n번째 피보나치 수인 F(n)은 F(n+2)에서 a값을 찾으면 되는 것이다.
반응형