프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
처음 시도한 코드
def isPrime(x):
count = [0] * (x+1)
for i in range(1, x+1):
for j in range(1, i+1):
if i % j == 0:
count[i] += 1
return count
def solution(number, limit, power):
return sum([power if i > limit else i for i in isPrime(number)])1부터 number까지의 수가 가지는 약수의 개수를 구하기 위해 isPrime(x) 함수를 만들었다.
count를 x+1의 길이로 만드는 이유는 리스트의 특성상 0번 인덱스부터 시작하기 때문에 1번부터 x번 인덱스까지 값을 담기 위함이다.
마지막에 sum을 할 때 0번 인덱스에 담긴 0은 결과값에 영향을 주지 않기 때문에 문제가 되지 않는다.
약수의 개수를 구하기 위해 나누어 떨어지면 count[i]에 +1을 해주었다.
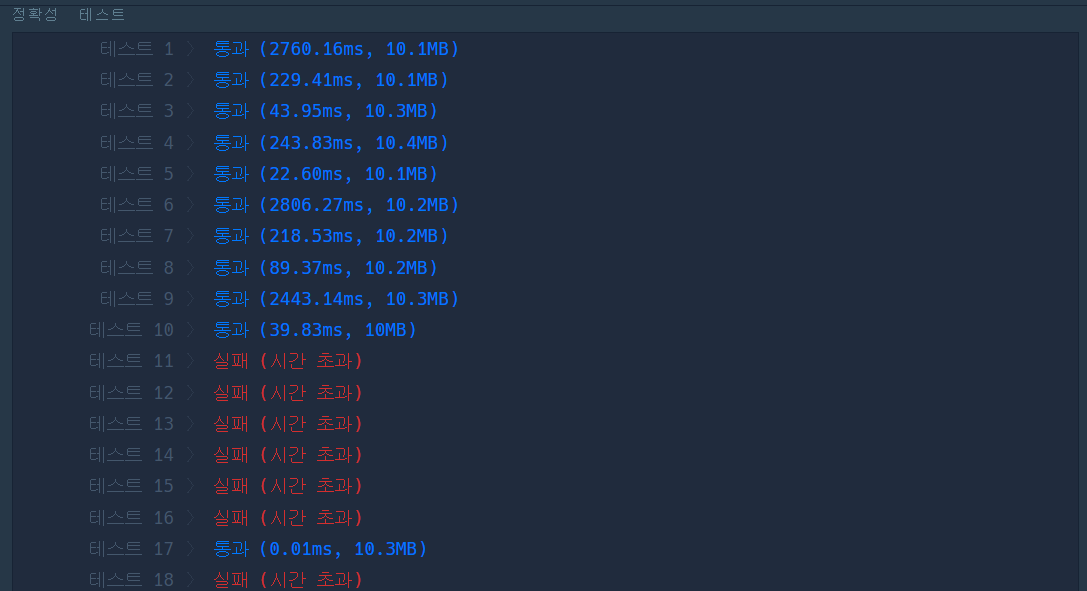
하지만, 이 코드는 number의 수가 커지면 커질 수록 for문에서의 시간도 증가하기 때문에 시간초과가 발생한다.

정답 코드
def isPrime(x):
count = [0] * (x+1)
for i in range(1, x+1):
for j in range(1, int(i**0.5)+1):
if i % j == 0:
if i / j == j:
count[i] += 1
else:
count[i] += 2
return count
def solution(number, limit, power):
return sum([power if i > limit else i for i in isPrime(number)])보통 약수에 관련된 문제가 나오면 시간 초과를 피하기 위해 i의 제곱근까지만 약수를 확인한다.
나 역시도 시간 초과를 해결하기 위해 j의 범위를 int(i**0.5)+1로 바꿔주었다.
하지만 약수인지 판별하는 것이 아닌, 해당 수의 모든 약수의 개수를 구해야 하기 때문에 count[i]에 +1을 하는 것이 불가능해진다.
만약, x가 15라면 x의 약수는 1, 3, 5, 15이고 총 4개이다.
15의 제곱근까지 약수를 판별하면 1, 3이 구해질 것이다. 1이 약수라는 것은 15도 약수라는 것이고, 3이 약수라는 것은 5가 약수라는 것과 같은 말이다.
따라서 약수의 개수가 짝수개이면 한개의 약수를 구할 때 count[i]에 +2를 해주면 된다.
반대로, x가 16이라면 x의 약수는 1, 2, 4, 8, 16으로 5개이고, 16의 제곱근까지 약수를 구하면 1, 2, 4가 구해질 것이다.
이렇게 약수의 개수가 홀수개인 경우에는 약수 하나를 구할 때마다 count[i]에 +2를 해줄 수 없다.
이 문제를 해결하기 위해 약수가 홀수개인 이유부터 찾아보면 제곱수일 경우임을 알 수 있다.
16은 4의 제곱이기 때문에 [1, 16], [2, 8]은 짝을 지을 수 있지만 [4]는 짝을 지을 수 없다.
따라서 해당 약수가 제곱근인지 판별하는 과정이 추가로 필요하다.
if i % j == 0: # 약수일 때
if i / j == j: # 제곱근이면(j*j=i) +1
count[i] += 1
else: # 아니면 +2
count[i] += 2j가 i의 약수인 경우에
- i를 j로 나눈 몫이 j이면, j는 i의 제곱근이므로 count[i]에+1를 해준다.
- 제곱근이 아니면 count[i]에 +2를 해준다.
이렇게 수정한 코드를 제출하면 틀리는 문제없이 모두 통과한다.