24416번: 알고리즘 수업 - 피보나치 수 1
오늘도 서준이는 동적 프로그래밍 수업 조교를 하고 있다. 아빠가 수업한 내용을 학생들이 잘 이해했는지 문제를 통해서 확인해보자. 오늘은 n의 피보나치 수를 재귀호출과 동적 프로그래밍
www.acmicpc.net
처음 시도한 코드
n = int(input())
f1, f2 = 0, 0 # 각 함수의 실행 횟수
def fib(n):
global f1
if n == 1 or n == 2:
f1 += 1
return 1
else:
return fib(n-1) + fib(n-2)
f = [0] * (n+1) # DP 테이블 초기화
def fibonacci(n):
f[1] = 1
f[2] = 1
global f2
for i in range(3, n+1):
f[i] = f[i-1] + f[i-2]
f2 += 1
return f[n]
# 각 함수 실행
fib(n)
fibonacci(n)
print(f1, f2)문제에서 주어진 의사코드를 토대로 작성한 코드이다.
코드 실행 횟수를 세기 위해 각 함수의 어디에서 실행 횟수를 카운트하면 될지 고민하다 아래와 같은 그림을 그려보았다.
재귀함수의 경우에는 1 또는 2가 되어 1을 리턴하는 횟수가 n번째 피보나치수 f(n)을 만들기 위한 함수 실행 횟수이다.
DP의 경우에는 f(n-1)+f(n-2)를 하는 횟수가 n번째 피보나치수 f(n)을 만들기 위한 함수 실행 횟수이다.
하지만 이 코드는 제출 시 시간 초과가 발생하기 때문에 좀 더 빠르게 답을 구하는 방법을 찾아야 했다.
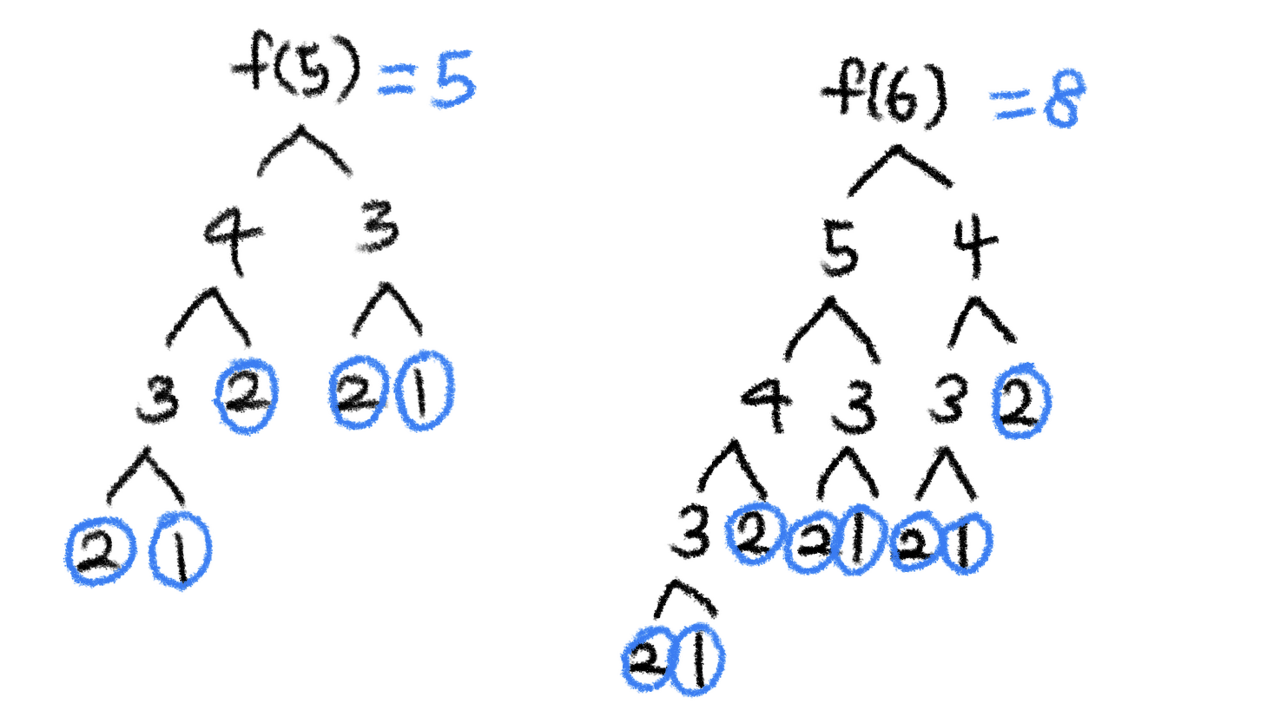

먼저, DP의 경우에는 f(1), f(2)는 1로 사전 정의가 되어 있기 때문에, f(1)과 f(2)를 만들 때는 함수를 실행하지 않는다.
따라서 f(n)을 구할 때는 n-2번의 함수 실행이 되는 것을 알 수 있다.
그럼 재귀함수를 사용하는 경우에는 어떻게 시간을 단축시킬 수 있을까?
코드
n = int(input())
def fib(n):
a, b = 1, 1 # f(1), f(2)
for _ in range(3, n+1): # 1, 2는 이미 정의했으므로 3부터 n까지
a, b = b, a+b
return b
def fibonacci(n):
return n-2
print(fib(n), fibonacci(n))시간초과가 발생하는 원인 중 하나가 재귀함수 호출이라고 생각했다.
그래서 함수를 계속해서 호출하지 않고 값을 저장하는 방법을 생각해 보다, swap을 사용하게 되었다.
def fib(n):
a, b = 1, 1 # f(1), f(2)
for i in range(3, n+1): # 1, 2는 이미 정의했으므로 3부터 n까지
a, b = b, a+b
return b이 코드로 fib(5)를 구하는 과정은 다음과 같다.
- i=3, a, b = 1, 1+1
- i= 4 a, b = 2, 1+2
- i=5, a, b = 3, 3+2
각 과정에서 a는 f(n-1)이 되고, b는 f(n) = f(n-1) + f(n-2)이 되는 것을 알 수 있다.
또한, f(n)의 값이 곧 재귀함수를 실행한 횟수가 된다.