1012번: 유기농 배추
차세대 영농인 한나는 강원도 고랭지에서 유기농 배추를 재배하기로 하였다. 농약을 쓰지 않고 배추를 재배하려면 배추를 해충으로부터 보호하는 것이 중요하기 때문에, 한나는 해충 방지에
www.acmicpc.net
코드
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
# dfs 정의
def dfs(x, y):
# 상하좌우
dx = [0, 0, -1, 1]
dy = [1, -1, 0, 0]
# 네 방향 탐색
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 범위 안에 있고 1이면(=배추이면) 지나간것을 -1로 표시하고 주변 탐색
if (0 <= nx < m) and (0 <= ny < n) and graph[ny][nx] == 1:
graph[ny][nx] = -1
dfs(nx, ny)
t = int(input()) # 테스트 케이스의 개수
for _ in range(t):
m, n, k = map(int, input().split()) # 가로, 세로, 배추 개수
graph = [[0 for _ in range(m)] for _ in range(n)]
# 배추 위치 표시
for _ in range(k):
X, Y = map(int, input().split())
graph[Y][X] = 1 # X, Y 바꿔서 표시해야하는거 주의!
# 배추 그룹 수(=배추흰지렁이 개수) 세기
count = 0
for a in range(m):
for b in range(n):
if graph[b][a] == 1:
dfs(a ,b)
count += 1
print(count)배추의 위치(=1)를 입력받아 graph에 나타낸다.
이때 배추의 위치는 x, y순으로 입력되지만, 실제 graph에서는 graph[y][x]에 1을 나타내야 한다.
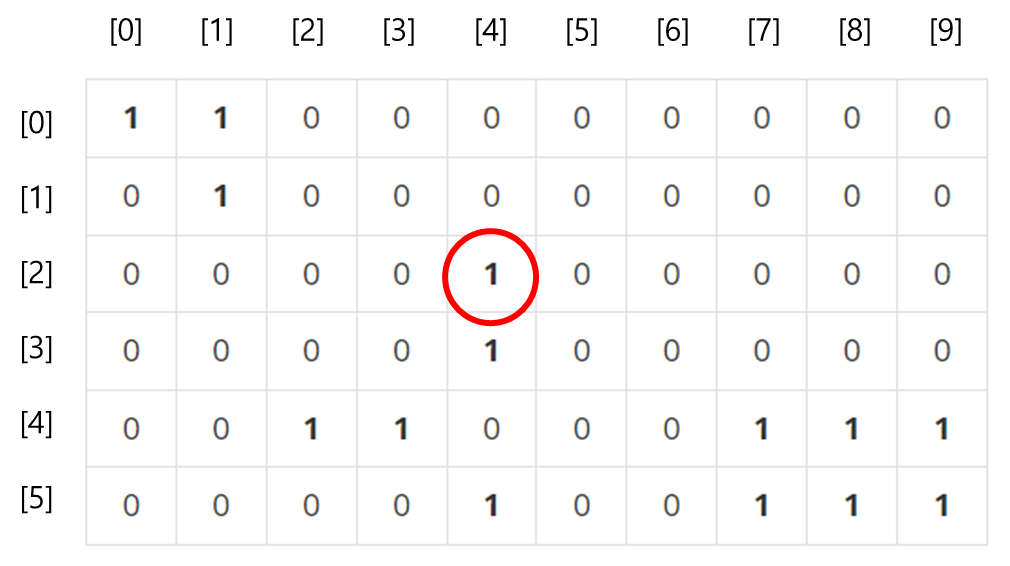
예를 들어, 아래와 같은 그림에서 빨간색 동그라미로 표시한 부분은 우리가 눈으로 보기에는 (가로, 세로) = (4, 2)이지만, graph는 2차원 배열이기 때문에 [행][열] 순으로 접근해야 한다.
그러므로 입력으로 (4, 2)이 주어지면 graph[2][4]에 1을 표시해주어야 한다.

모든 배추의 위치 표시가 완료되면 필요한 배추흰나방의 개수, 즉 배추구역의 개수를 센다.
graph를 탐색하며 해당 위치가 배추(=1)이면 dfs를 수행하고 완료되면 count+1을 한다.
dfs 함수는 내부에서 dfs 함수를 계속해서 재귀 호출하기 때문에 다음과 같이 재귀 최대 깊이(resursionlimit)를 설정해주어야 한다.
import sys
sys.setrecursionlimit(10**6)
dfs 함수는 다음과 같이 정의하였다.
# dfs 정의
def dfs(x, y):
# 상하좌우
dx = [0, 0, -1, 1]
dy = [1, -1, 0, 0]
# 네 방향 탐색
for i in range(4):
nx = x + dx[i]
ny = y + dy[i]
# 범위 안에 있고 1이면(=배추이면) 지나간것을 -1로 표시하고 주변 탐색
if (0 <= nx < m) and (0 <= ny < n) and graph[ny][nx] == 1:
graph[ny][nx] = -1
dfs(nx, ny)매개변수로 x, y 좌표가 전달되면 해당 좌표에서 상하좌우를 탐색한다.
이동한 좌표 nx, ny가 그래프 범위 안에 존재하고, 1이면(=배추이면) 해당 위치의 값을 -1로 바꿔 지나간 것으로 표시하고 그 위치에서 다시 dfs함수를 호출한다.
(x, y)에서 주변 배추(=1)를 모두 탐색해 더 이상 1이 존재하지 않으면 그때 count를 +1 하여 한 구역(=배추흰나방의 개수)이 완료되었음을 알 수 있다.