깊이 우선 탐색(DFS; Depth-First search)
그래프의 시작 노드에서 출발하여 탐색할 한쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후 다른 쪽 분기로 이동하여 다시 탐색을 수행하는 알고리즘
- 재귀 함수로 구현
- 스택 자료구조 이용
- 시간 복잡도(노드 수: V, 에지수: E) $O(V + E)$
- 풀 수 있는 문제: 단절점 찾기, 단절선 찾기, 사이클 찾기, 위상 정렬
1. DFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
- 인접 리스트로 그래프 표현하기
- 방문 리스트 초기화하기
- 시작 노드 스택에 append()로 삽입하기

2. 스택에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 스택에 삽입하기
- pop()으로 노드 꺼내기
- 꺼낸 노드를 탐색 순서에 기입
- 인접 리스트의 인접 노드를 스택에 삽입하여 방문 배열 체크

3. 스택 자료구조에 값이 없을 때까지 반복하기
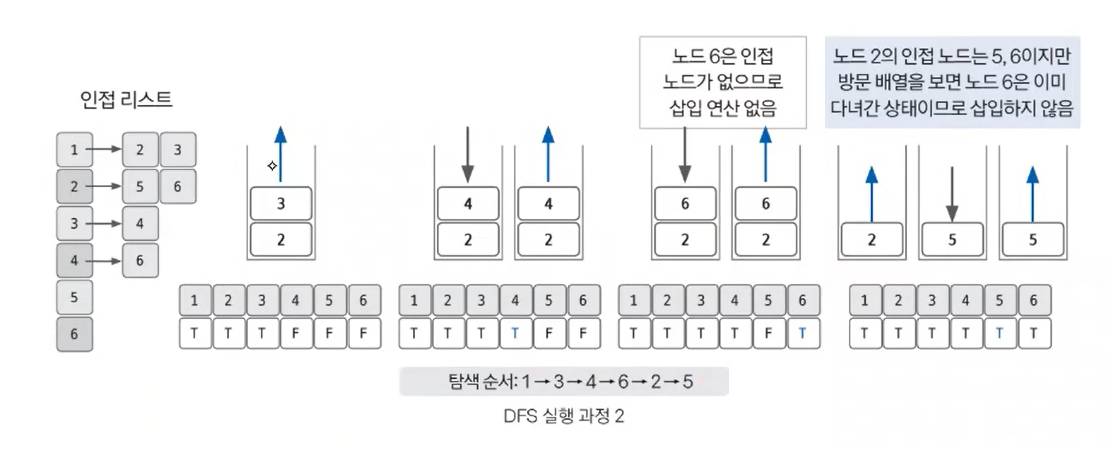
- 스택에서 3을 꺼내 탐색 순서에 기록 → 인접 노드 4 스택에 삽입 및 방문 배열에 체크
- 4를 꺼내 탐색 순서에 기록 → 인접 노드 6 삽입 및 방문 배열에 체크
- 6을 꺼내 탐색 순서에 기록 → 인접 노드 없으므로 추가 삽입 없음
- 2를 꺼내 탐색 순서에 기록 → 인접 노드 5, 6 방문 여부 확인
- 이때, 6은 이미 방문 배열에 T로 체크되어 있으므로 5만 삽입 및 방문 배열에 체크
- 5를 꺼내 탐색 순서에 기록 → 인접 노드 없으므로 추가 삽입 없음
- 스택이 비었으므로 과정 종료
💡 스택에 노드를 삽입(append)할 때 방문 배열 체크
💡 스택에서 노드를 뺄(pop) 때 탐색 순서에 기록
import sys
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n, m = map(int, input().split()) # 사람의 수, 친구 관계의 수
# 그래프 정보
graph = [[] for _ in range(n)]
for _ in range(m):
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
visited = [False] * n # 방문 배열
answer = False # 주르륵 5명이 친구인 A-B-C-D-E가 존재하는지
# DFS 함수
def DFS(x, count):
global answer
# 5개가 되면 answer=True로 변경한 후 함수 종료
if count == 5:
answer = True
return
visited[x] = True
for i in graph[x]:
if not visited[i]:
DFS(i, count+1) # DFS 탐색 시 친구 수와 함께 넘겨줌
# 종료조건이 아니라면 다른 노드로부터 재탐색이 이뤄지므로 False로 바꿔줌
visited[x] = False
# 모든 노드에 대해 DFS를 수행
for i in range(n):
DFS(i, 1)
if answer:
print(1)
break
else:
print(0)
너비 우선 탐색(BFS; Breadth-First Search)
시작 노드에서 출발해 시작 노드를 기준으로 가까운 노드를 먼저 방문하면서 탐색하는 알고리즘
- FIFO 탐색
- 큐 자료구조 이용
- 시간 복잡도(노드 수: V, 에지 수: E) $O(V+E)$
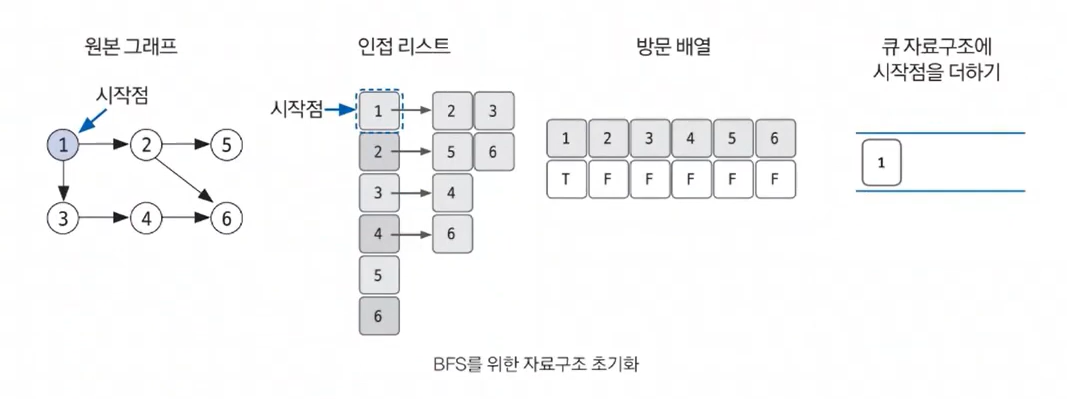
1. BFS를 시작할 노드를 정한 후 사용할 자료구조 초기화하기
- 인접 리스트로 그래프 표현하기
- 방문 리스트 초기화하기
- 시작 노드 큐에 append()로 삽입하기
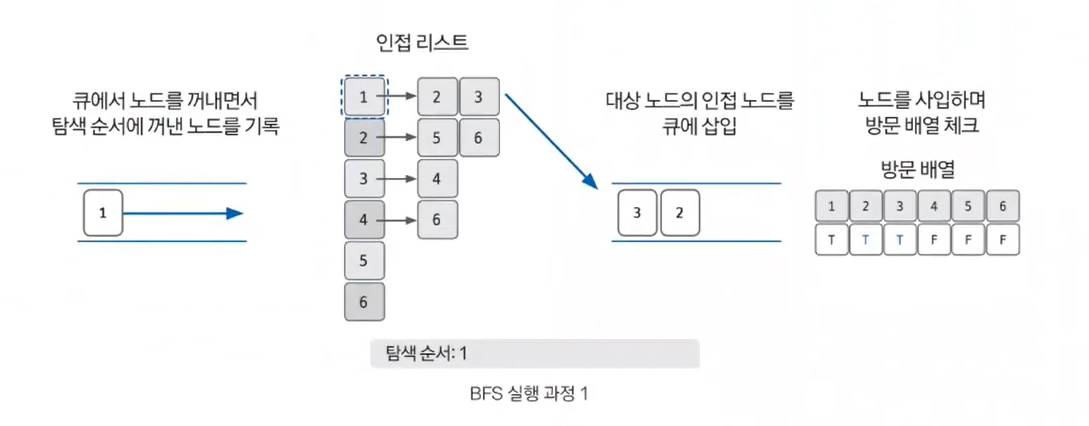
2. 큐에서 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 큐에 삽입하기
- pop()으로 노드 꺼내기
- 꺼낸 노드를 탐색 순서에 기입
- 인접 리스트의 인접 노드를 큐에 삽입하여 방문 배열 체크
3. 큐 자료구조에 값이 없을 때까지 반복하기
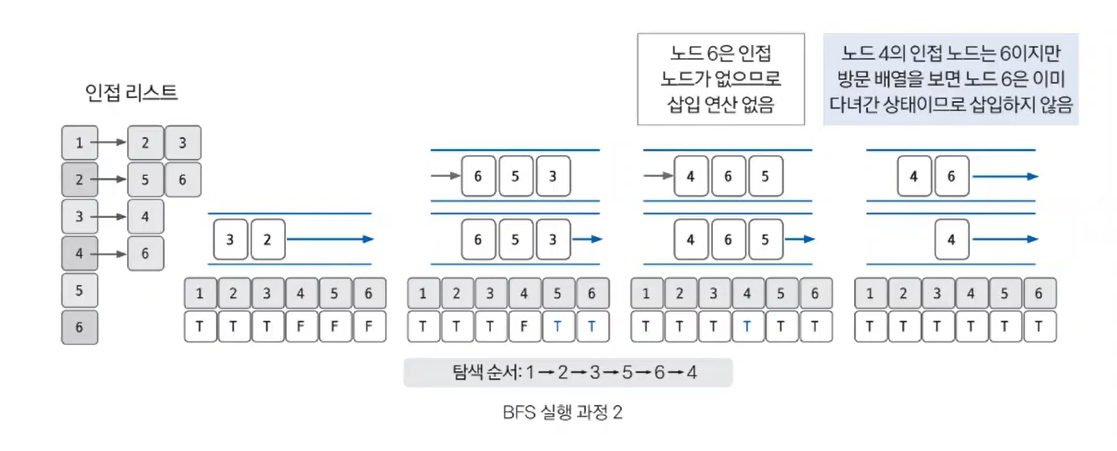
- 노드 2를 꺼내 탐색 순서에 기입 → 인접 노드 5, 6을 큐에 삽입하고 방문 배열 체크
- 노드 3을 꺼내 탐색 순서에 기입 → 인접 노드 4를 큐에 삽입하고 방문 배열 체크
- 노드 5를 꺼내 탐색 순서에 기입 → 인접 노드 없음
- 노드 6을 꺼내 탐색 순서에 기입 → 인접 노드 없음
- 노드 4를 꺼내 탐색 순서에 기입 → 인접 노드 6 방문 여부 확인
- 이때, 노드 6은 이미 방문 배열에 T로 표시되어 있으므로 삽입하지 않음
- 큐가 비었으므로 과정 종료
from collections import deque
n, m = map(int, input().split())
# 그래프 정보
graph = []
for i in range(n):
graph.append(list(map(int, input())))
dx = [0, 0, 1, -1]
dy = [1, -1, 0, 0]
def BFS(i, j):
queue = deque()
queue.append((i, j))
while queue:
x, y = queue.popleft()
# 상하좌우로 이동
for k in range(4):
nx = x + dx[k]
ny = y + dy[k]
# # 범위 안에 있을 때
if 0 <= nx < n and 0 <= ny < m:
# 이동할 수 있는 칸이면(=1)
if graph[nx][ny] == 1:
graph[nx][ny] = graph[x][y] + 1 # 방문 했다는 표시로 +1을 해줌
queue.append((nx, ny))
return graph[n-1][m-1]
print(BFS(0, 0))
# BFS
import sys
from collections import deque
sys.setrecursionlimit(10**6)
input = sys.stdin.readline
n = int(input()) # 정점의 개수
# 그래프 정보
graph = [[] for _ in range(n+1)]
for _ in range(n):
tree = list(map(int, input().split()))
for i in range(1, len(tree)//2):
graph[tree[0]].append((tree[2*i-1], tree[2*i]))
# BFS 함수
def BFS(x):
queue = deque([x])
visited[x] = True
while queue:
now = queue.popleft()
for i, w in graph[now]:
if not visited[i]:
queue.append((i))
visited[i] = True
distance[i] = distance[now] + w
# 루트 노드(1)에서의 각 정점까지의 거리 계산
visited = [False] * (n+1)
distance = [0] * (n+1)
BFS(1)
max_distance = max(distance) # 최장 거리
max_node = distance.index(max_distance) # 해당 노드
# max_node에서 시작해 각 정점까지의 거리 계산
visited = [False] * (n+1)
distance = [0] * (n+1)
BFS(max_node)
print(max(distance))
반응형