3주차 | 문제 3. 구름이의 여행
문제
구름이가 사는 구름 나라는 N개의 섬으로 이루어져 있습니다. 각 섬에는 1부터 N까지의 번호가 붙어 있고, 구름 나라는 사람들이 섬과 섬 사이를 편하게 이동할 수 있도록 다리를 M개 설치했습니다.
설치된 다리들은 아래의 특징들을 만족합니다.
- 모든 다리는 양방향으로 이동할 수 있습니다.
- 서로 다른 두 섬을 잇는 다리는 최대 하나입니다.
- 다리가 잇는 두 섬은 항상 다른 섬입니다.
구름이는 1번 섬에서 출발해서 N번 섬으로 가려고 하는데, 통과하는 다리의 개수가 K개 이하가 되길 원합니다. 구름이를 도와 1번 섬에서 N번 섬까지 K개 이하의 다리만을 이용해 도착할 수 있는지를 구해봅시다.
예시
첫 번째 예시를 그래프로 나타내보면 아래 그림과 같습니다.

다리의 배치가 위와 같을 때, 1 > 2 > 6 , 1 > 3 > 4 > 1 > 2 > 6 , 1 > 4 > 2 > 6 과 같은 방법으로 1번 섬에서 6번 섬으로 이동할 수 있습니다. 이 외에 같은 다리를 여러 번 이용할 수도 있으므로, 6번 섬으로 갈 수 있는 다양한 경로가 존재합니다. 이러한 경로들 중, 1 > 2 > 6 의 경로를 이용하면 2개의 다리만을 이용해 6번 섬에 도착할 수 있으므로 예시의 정답은 YES가 됩니다.
입력
첫째 줄에 섬의 개수 N(2≤N≤1,000)과 다리의 개수 M(1≤M≤5,000), 그리고 구름이가 건널 최대 다리의 개수를 의미하는 K(1≤K≤M)가 공백으로 구분되어 주어집니다. 다음 M개의 줄에는 다리가 잇는 두 섬의 번호를 의미하는 u,v(1≤u,v≤N)가 공백으로 구분되어 주어집니다.
입력에서 주어지는 모든 수는 정수입니다.
출력
구름이가 1번 섬에서 N번 섬까지 K개 이하 의 다리를 사용해서 갈 수 있다면 YES, 갈 수 없다면 NO를 출력합니다.
그래프 문제는 처음 풀어보게 되어 접근조차 어려웠다^^;; 앞으로 계속해서 그래프문제가 출제될 예정이라는데...
구름 해설을 토대로 이해한 바를 정리하는 내용으로 작성되어 명확하지 않을 수 있음을 미리 알립니다.
defaultdict를 이용하여 양방향 그래프 만들기
defaultdict는 주어지는 키가 없다면 자동으로 생성하고 지정한 비어있는 자료형을 바로 할당한다.
# 양방향 그래프
n = 3
from collections import defaultdict
graph = defaultdict(list)
for i in range(n):
s, e = map(int, input().split()) # 출발노드, 도착노드 (=연결된 두 노드)
graph[s].append(e) # 출발 -> 도착
graph[e].append(s) # 도착 -> 출발
print(graph)
# result
# defaultdict(<class 'list'>, {1: [2, 3], 2: [1, 3], 3: [2, 1]})- s, e라는 이름으로 연결된 두 노드를 입력받아 graph이름으로 선언한 defaultdict에 연결된 두 노드를 추가해준다.
- 양방향 그래프이므로 출도착을 바꿔 각각 저장해주어야 한다.
- 1, 2 / 1, 3 / 2, 3이 입력되면 graph에는 {1: [2, 3], 2: [1, 3], 3: [2, 1]}과 같이 데이터가 저장된다.
- defaultdict의 각 키에는 연결된 노드의 정보가 저장된다. ex) 1 : [2,3] -> 1번노드는 2번, 3번 노드와 연결되어 있다는 의미
너비 우선 탐색; BFS(Breadth-Frist-Search)
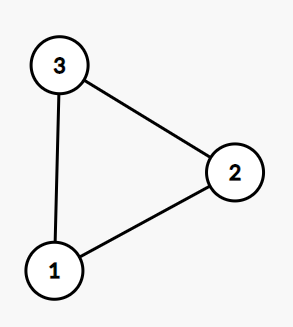
너비 우선 탐색은 특정 노드에서 경로를 찾거나, 최단 거리를 찾으려고 할 때 자주 사용되는 방법으로, 이 문제의 경우 1번 섬에서 N번 섬으로 K개 이하의 다리를 이용해서 가는 경로를 찾아 있으면 YES를 출력하는 문제이므로 BFS를 이용해 해결할 수 있다.
BFS는 FIFO(First-In-First-Out)방식의 Queue를 이용하여 구현할 수 있다.
왼쪽 그림과 같은 양방향 그래프가 있을 때, BFS를 코드를 통해 구현하면 다음과 같다.
q = deque() # 데크 생성
q.append(1) # 1번 노드 추가(현재 위치)
cur = q.popleft() # 맨 앞의 값을 빼온다.
q.append(graph[cur]) # 빼온 값에 해당하는 연결된 노드를 데크에 추가
next = q.popleft() # 다음 값(위에서 추가한 값)을 선택
for i in next:
print("%d번 노트에는 %d번 노드로 가는 간선이 있습니다."%(cur, i))
q.append(i) #도착지점 노드를 현재 노드 관리 자료형 Queue에 추가
cur = q.popleft()
print("현재 노드는 %d 입니다."%(cur))
# 현재 노드는 2 입니다.- q라는 이름으로 deque를 만든다. **queue는 단방향 접근인 반면, deque는 양방향 접근이 가능한 자료형이다.
- 1번 노드에서 시작하기 위해 q에 1번 노드를 추가해주고 q의 맨앞에 위치한 1번노드를 popleft() 통해 가지고 온다.
- 가져온 1번 노드(cur)에 대한 연결 정보를 graph에서 찾아 q에 추가해준다. => q에는 2번, 3번 노드가 저장되어 있음(1번 노드는 popleft()를 통해 지워짐)
- 또 다시 popleft()를 통해 2번, 3번 노드를 가지고 온다. 이때 데이터는 리스트로 묶여있다.
- 가져온 데이터(next)를 통해 for문을 돌리면 1번 노드(cur)와 연결된 노드(i)를 q에 추가한다.
- q에서 popleft()를 통해 맨 앞 데이터를 가져와 cur를 갱신하여 다음 노드로 이동한다.
방문 횟수를 기록하는 visited 변수
각 노드에 연결된 다리를 이용한 횟수를 기록하기 위한 visited 변수를 선언한다.
이 변수는 방문 여부와 거리를 관리하며
- 방문한 적이 없으면 Visited 값은 -1
- 방문한 적이 있으면 현재의 다리 이용 횟수 + 1
- 1번부터 5번까지의 노드가 있고 이때 Vistied = [0, 0, 0, 0, 0] 이라고 가정한다면, Visited[3]의 값은 3번 노드까지 사용한 다리의 최소 개수를 보관한다.
따라서, visited 변수를 이용하여 k 이하 값을 가지는 노드만 조건문으로 판단해주면 원하는 출력 결과를 얻을 수 있다.
구름 정답 코드
import sys
from collections import defaultdict
from collections import deque
n,m,k=map(int,sys.stdin.readline().split()) # 섬의 개수, 다리의 개수, 최대 다리의 개수
dict=defaultdict(list) # 연결된 두 섬을 입력받을 defaultdict
for _ in range(m): # 다리의 개수만큼 반복
u,v=map(int,sys.stdin.readline().split()) # 연결된 두 섬을 입력받아
dict[u].append(v) # dict에 각각 연결된 섬을 추가해줌
dict[v].append(u)
q=deque() # 이동을 판별하기 위한 데크 생성
visited=[-1 for _ in range(n+1)] # 다리이용횟수: 모든 다리를 사용하지 않은 상태(-1)로 시작
# 1번섬~n번섬이므로 n+1개로 만들어 인덱싱에 편리하게 함
visited[1]=0 # 1번 섬에서 시작하므로 1번 섬의 다리 이용 횟수를 0으로 바꿔주고
q.append(1) # q에 1번섬 추가
while q: # q에 값이 존재하면 계속해서 반복
cur=q.popleft() # 제일 앞에 위치한 값을 가져옴=현재 위치한 노드
for next in dict[cur]: # 현재 위치한 노드에 해당하는 dict값(=연결된 섬)을 가져와
if visited[next] != -1: # 다음 노드로 연결된 다리를 사용했으면(-1이 아니면)
continue
# 사용하지 않았으면(-1이면)
q.append(next) # 연결된 노드를 q에 추가(=다음 노드로 이동)
visited[next]=visited[cur]+1 # 현재노드의 다리이용횟수+1을 연결된 노드의 다리이용횟수로 저장
if 1 <= visited[n] <= k: # k개 이하의 다리를 사용해서 갈 수 있으면 YES
print('YES')
else: # 갈 수 없으면 NO
print('NO')